Computing the Posterior

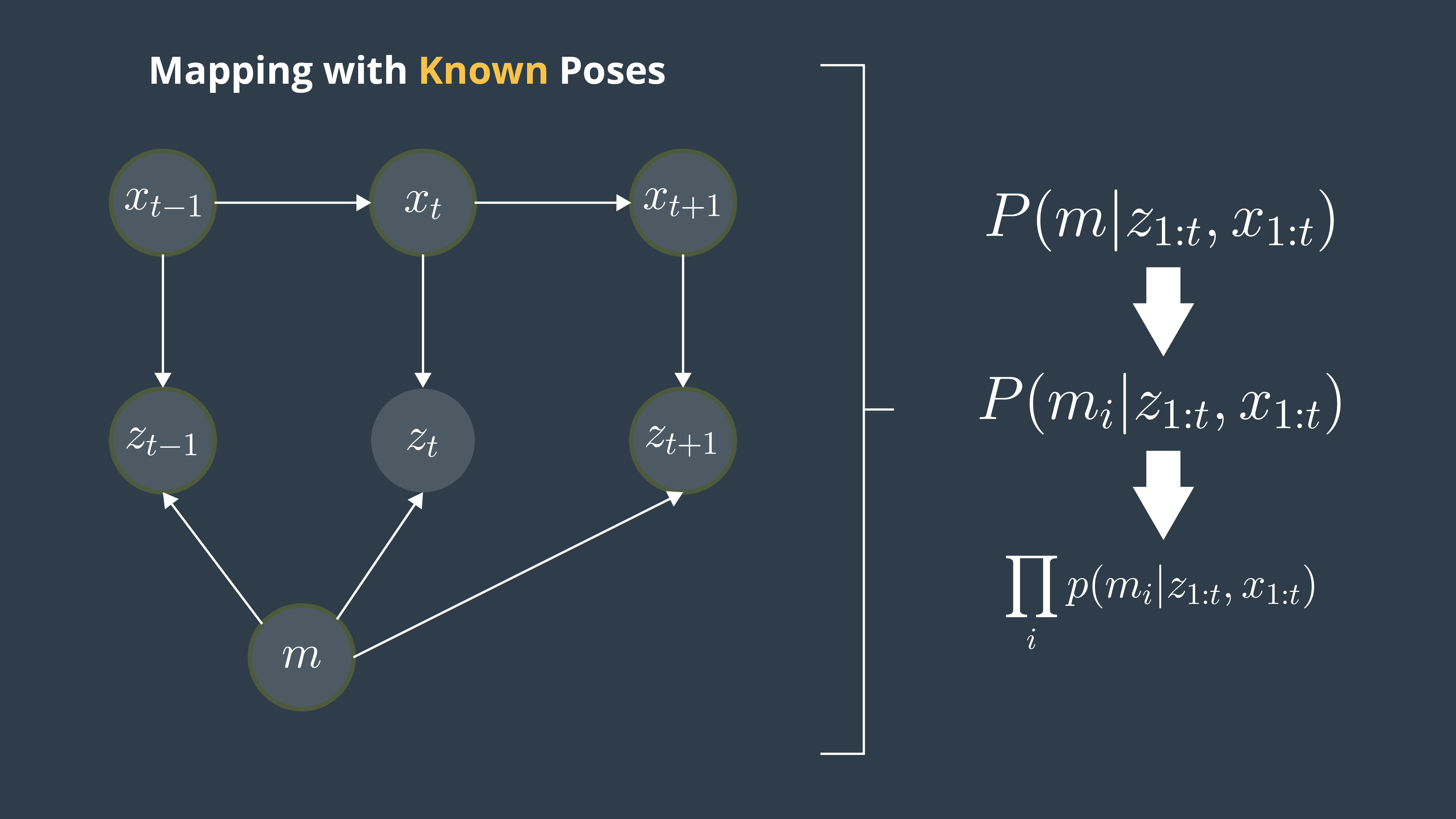
First\ Approach: P(m | z_{1:t}, x_{1:t})

We just saw that maps have high dimensionality so it will be too pricey in terms of computational memory to compute the posterior under this first approach.

Second\ Approach:P(m_{i} | z_{1:t}, x_{1:t})

A second or better approach to estimating the posterior map is to decompose this problem into many separate problems. In each of these problems, we will compute the posterior map m _i at each instant.
However, this approach still presents some drawbacks because we are computing the probability of each cell independently. Thus, we still need to find a different approach that addresses the dependencies between neighboring cells.

Third\ Approach:\prod_{i} P( m_{i}| z_{1:t} , x_{1:t})

Now, the third approach is the best approach to computing the posterior map by relating cells and overcoming the huge computational memory, is to estimate the map with the product of marginals or factorization.

In this quiz, we'll get you back to your calculus where you will try to remember how to evaluate this function:

\prod_{P=0.7}^{1.0}\ P^{2}

step = 0.1

0.154016

0.7

1

0.254016

1.7

0.5312

SOLUTION:

0.254016